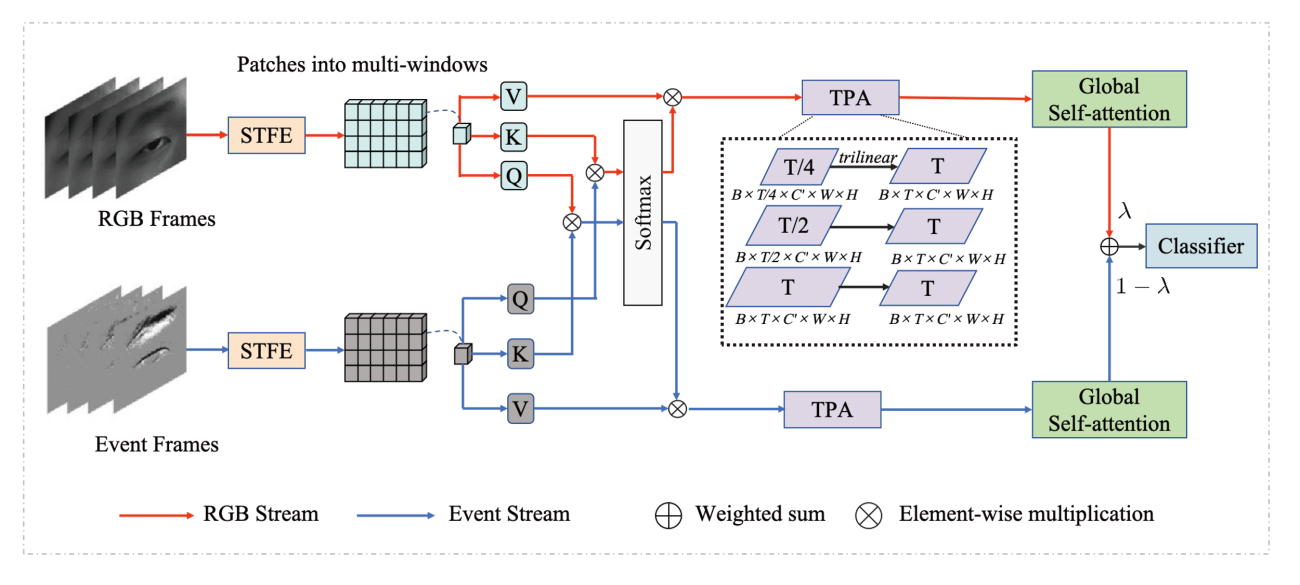
Recognizing emotions from a single eye has been a hard work over time, mainly because muscle movements are hard to perceive and event data is susceptible to noise. Most existing methods concentrated on semantic fusion, neglecting the potential benefits of local interaction between different modalities. Considering this problem, we design a new framework called HEC-Net which hierarchically fuses different modalities’ information. Our HEC-Net begins with a dual-stream Spatio-Temporal Feature Extraction (STFE) module to encode texture and motion while suppressing noise via Top-k selection, which follows a “perceive and select” design philosophy. Then we form a three-stage local-to-global fusion process to fuse the information in a more layered approach. The whole approach includes a multi-window fusion, a pyramid structure and a global fusion. The multi-window fusion constrains interactions locally, enabling the model to firstly concentrate on details. We employ a pyramid structure to capture the changes in blinking actions over time. Finally, the global fusion process aggregates dispersed cues into a coherent global representation. HEC-Net achieves a state-of-the-art UAR of 92.30% on the SEE dataset, which remains stable and efficient under various lighting conditions.



